Project Niagara UNB Data Challenge 2021
The ever-dynamic Asian telecommunication industry is facing stiff competition amongst service providers with rapid introduction of innovative features and services such as airtime transfer, data sharing, mobile money, location aware apps, advanced social networking, and several OTT services. Fast growing telecom market in developing Asian countries is primarily a prepaid connections market. Among the various ways to reload a prepaid mobile phone through a refill card, online bank transfer, electronic reload at convenient store etc. peer to peer airtime transfer is emerging as a popular option. Peer to peer transfer involves a subscriber A transfer a part of their balance to subscriber B which can then be used for data, SMS, or voice call.
Challenge
The airtime transfer can be done in two ways: direct transfer and accepting a request for a transfer. Direct transfer involves a subscriber A initiating a transfer directly to subscriber B. Request transfer involves subscriber B raising a request for a certain amount from subscriber A and then subscriber A either accepts or rejects the transfer request. Typically, the transfer is done through an SMS in a specific format to a toll-free number. Many a times the transfer fails for variety of reasons such as incorrect amount (Only integer amount of $1 - $25 is allowed), incorrect mobile number, sending airtime to a post postpaid number, technical glitches etc. The objective of this data challenge is to characterize the users and identify the drivers of airtime transfer to enhance the count and value of successful transactions.
[Show me the Code]
Let’s start by dividing the columns into meta data (transactions) and customer data to avoid confusion.
cust_df = pd.DataFrame()
cust_df['uid'] = df.uid
cust_df['cnt_uid'] = df.cnt_uid
cust_df['activedays'] = df.activedays
cust_df['total_amt'] = df.total_amount
transaction_cols = [i for i in df.columns if 'mn' in i]
transactions_df = df.loc[:, ['uid'] + transaction_cols[8:]]
Also, since the data was collected in a real-time environment, there are a few cases where there are inconsistencies in the columns like tx and success which indicate the total number of transactions and total number of successful transactions respectively. Therefore, these columns are re-calculated from the rest of the data provided
Note: This information was verified by the moderator of the competition.
cust_df['tx'] = transactions_df.iloc[:,1:9].sum(axis=1)
cust_df['suc_tx'] = transactions_df.iloc[:,17:].sum(axis=1)
We start by investigating the transaction data, firstly let’s check whether there are any users who don’t have a single successful transaction
cust_df[cust_df.suc_tx == 0].shape[0] / cust_df.shape[0]
0.37119894148277777
Interestingly, 37% users don’t even have a single successful transaction
Since, the customer-level transaction data is given for a period of 8 months, it would be interesting to see the month-wise trend in the data. This calculation is a bit complex and involves grouping and slicing operations.
Here’s a look at the table
| tx_type | ra | rb | ta | tb |
|---|---|---|---|---|
| month | ||||
| 1 | 634246 | 634246 | 7372594 | 7373422 |
| 2 | 507185 | 507184 | 6342612 | 6343615 |
| 3 | 538862 | 538862 | 6759832 | 6760975 |
| 4 | 490808 | 490807 | 6034889 | 6035866 |
| 5 | 478420 | 478418 | 6081518 | 6082517 |
| 6 | 405210 | 405210 | 5340496 | 5341387 |
| 7 | 406012 | 407809 | 5246627 | 5248129 |
| 8 | 52292 | 52528 | 673933 | 674155 |
Now for the trend
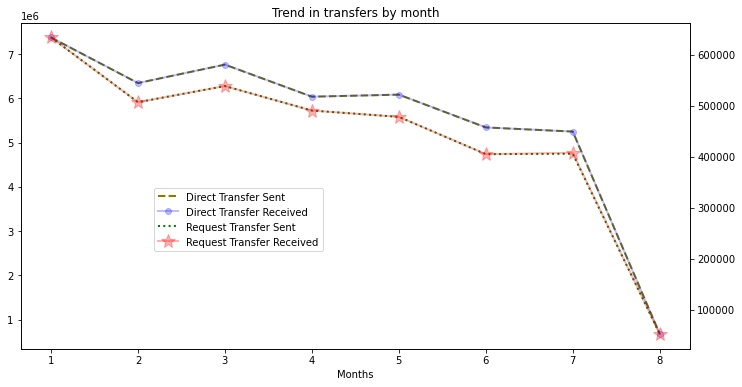
Overall there is a decreasing trend in the number of transactions across months
Previously created table would also help us determine what proportion of transactions are successful
total_tx = transactions_df.iloc[:,1:9].sum()
tx_mn.suc_tx.sum() / total_tx.sum()
0.2586547689367111
On average, only 1 in 4 transaction is successful.
Let’s also have a look at the proportion of direct and request transfers in our dataset
array([0.9258175, 0.0741825])
Here the values denote number of direct and request transfers respectively. Large proportion of customers prefer direct transfers over request transfers
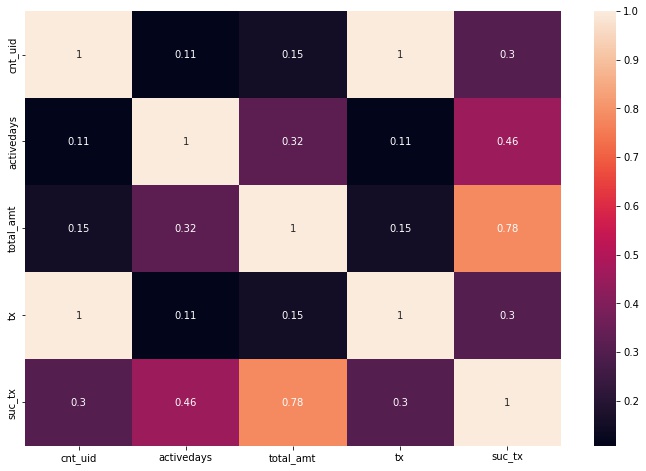
Now that we understand the customer transactions better, let’s have a look at the customer table and analyze if there’s any relationship between the variables. More specifically we’re aiming to see if any linear relationship exists among the columns.
pearsonr(cust_df.suc_tx, cust_df.total_amt)
(0.7827031132599644, 0.0)
-
The above values indicate the correlation between successful transactions and the total amount transferred for a particular customer, and its corresponding p-value respectively. The values indicate that there is a significantly strong positive correlation between these columns.
-
Also, from the heatmap it can be observed that majority of the transactions involve new people as
cnt_uidcolumn has a positive correlation with the total number of transactions.
Let’s characterize the users using clustering. More specifically using KMeans clustering methodology. It is crucial to normalize the columns during preprocessing due to different scales, as KMeans is a distance-based algorithm
scaler = preprocessing.MinMaxScaler()
scaled_arr = scaler.fit_transform(cust_df)
scaled_arr.shape
(9371600, 6)
We use elbow-plot to determine the optimal number of clusters for KMeans
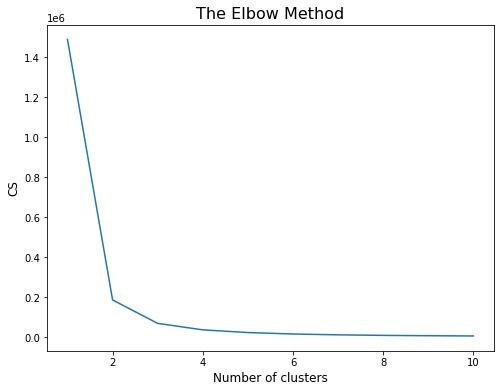
We observe from the above plot that 3 would be the optimal number of clusters for our case.
Fitting the algorithm…
KMeans(n_clusters=3, random_state=42)
Here’s a look at the clusters and its characterics for different columns
| cnt_uid | activedays | total_amt | tx | suc_tx | |
|---|---|---|---|---|---|
| cluster | |||||
| 0 | 4.327881 | 7.333546 | 6.427707 | 4.325501 | 1.112377 |
| 1 | 92.512831 | 193.516409 | 55.570050 | 91.677877 | 23.953850 |
| 2 | 25.305886 | 96.190044 | 20.740651 | 25.179140 | 6.021600 |
The clusters are quite different from each other with respect to the mean value of the features. However let’s check if these differences are significant using ANOVA
Col = cnt_uid
df sum_sq mean_sq F PR(>F)
C(cluster) 2.0 1.522260e+10 7.611302e+09 47570.489501 0.0
Residual 9371597.0 1.499460e+12 1.600005e+05 NaN NaN
group1 group2 Diff Lower Upper q-value p-value
0 2 0 20.978005 20.110581 21.845429 80.158685 0.001
1 2 1 67.206945 66.303296 68.110595 246.508642 0.001
2 0 1 88.184951 87.506381 88.863520 430.742777 0.001
Col = activedays
df sum_sq mean_sq F PR(>F)
C(cluster) 2.0 6.626394e+10 3.313197e+10 9.790829e+07 0.0
Residual 9371597.0 3.171330e+09 3.383980e+02 NaN NaN
group1 group2 Diff Lower Upper q-value p-value
0 2 0 88.856498 88.816606 88.896390 7382.821651 0.001
1 2 1 97.326366 97.284808 97.367923 7762.387032 0.001
2 0 1 186.182864 186.151657 186.214070 19774.705623 0.001
Col = total_amt
df sum_sq mean_sq F PR(>F)
C(cluster) 2.0 4.670997e+09 2.335498e+09 472249.958543 0.0
Residual 9371597.0 4.634696e+10 4.945471e+03 NaN NaN
group1 group2 Diff Lower Upper q-value p-value
0 2 0 14.312944 14.160442 14.465445 311.080081 0.001
1 2 1 34.829399 34.670529 34.988270 726.642547 0.001
2 0 1 49.142343 49.023044 49.261642 1365.325600 0.001
Col = tx
df sum_sq mean_sq F PR(>F)
C(cluster) 2.0 1.493326e+10 7.466632e+09 46680.592349 0.0
Residual 9371597.0 1.499001e+12 1.599515e+05 NaN NaN
group1 group2 Diff Lower Upper q-value p-value
0 2 0 20.853640 19.986348 21.720931 79.695670 0.001
1 2 1 66.498737 65.595226 67.402248 243.948337 0.001
2 0 1 87.352376 86.673911 88.030842 426.741347 0.001
Col = suc_tx
df sum_sq mean_sq F PR(>F)
C(cluster) 2.0 1.027724e+09 5.138621e+08 1.059767e+06 0.0
Residual 9371597.0 4.544122e+09 4.848823e+02 NaN NaN
group1 group2 Diff Lower Upper q-value p-value
0 2 0 4.909222 4.861471 4.956974 340.754495 0.001
1 2 1 17.932250 17.882504 17.981996 1194.800167 0.001
2 0 1 22.841473 22.804117 22.878828 2026.703045 0.001
The above table shows the signifance of the difference between clusters for various columns and also shows which clusters are different from each other using Tukey’s HSD Test.
Let’s move on to the second part of the problem where we determine the factors that affect the count and value of a successful transaction.
We have already identified that count and value of a successful transaction are correlated therefore we exclude total_amt column from the analysis and build a model on the following features to study its effect on the target (num of successful transactions):
cnt_uidactivedaystx
In order to study the effect of different features on the number of successful transactions, a transaction first has to be successful. Therefore we’ll subset the dataframe to include only those transactions which were successful.
suc_tx = cust_df[cust_df.suc_tx > 0]
Let’s plot the distribution of our target.
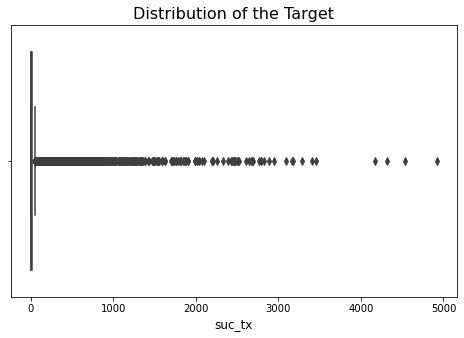
The target seems to be heavily skewed and there are a lot of outliers in the data. However, upon investigation it was found that these outliers were actual data points and not errors therefore it doesn’t make sense to exlcude them from the analysis.
Moreover, since the data is not normally distributed and due to lack of linear relationships between the target and the independant variables, we’ll employ a tree based model.
Let’s split the dataset into training and testing sets. Due to a huge amount of data and limited time, we’l only split the dataset into a train and test set.
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.30, random_state=42)
Now, training our Decision Tree Regressor
DecisionTreeRegressor(max_depth=7, random_state=49)
Here’s look at the feature importances
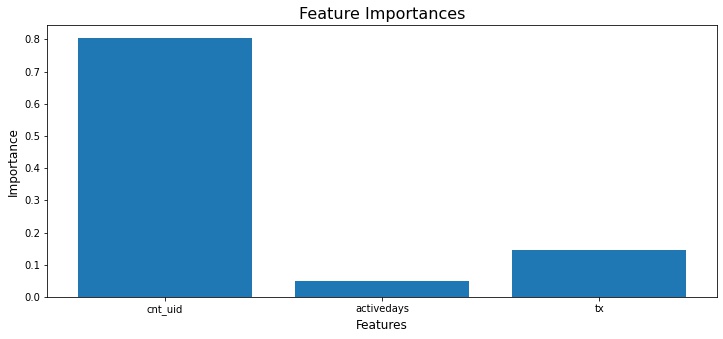
Interestingly, the number of distinct persons with whom a customer has engaged is ranked highest, while the number of days a it has been active on the network is ranked lowest.
Conclusion
- Cluster 1 was identified as a persona with the high value and more distinct transactions. This persona also interacts with new people more.
- Cluster 2 consists of moderately engaged customers, an important goal for the business here would be to try to move these users into Cluster 1 by leveraging marketing efforts.
- My first suggestion in order to drive the count and value of a successful transactions would be to improve the quality of the data by adding in features that determines the major reason behind an unsuccesful transaction.
- Furthermore, as seen above, the value of a transaction has a strong positive correlation with the count, implying that enhancing one can boost the other.
- Encouraging a customer to make more unique transactions will help boost the number of successful transactions, therefore enhancing the value of a transaction.